散布図とは?
散布図には、様々な使い方があります。
2つの変数のデータを平面にプロットすることで、その関係性を見るために使われるのが一般的です。
しかし、視点を変えると、散布図の使い方は様々なものがあります。
(A)2つの変数データの相関の有無を調べる
(B)相関が明確な2つの変数データの分布をみる
(C)2つの変数データを使って、平面上に図形を描く
(D)分布されたデータの図、様々な使い方
通常に使用される散布図は、(A)の「相関をみる散布図」使い方でしょう。
(C)の使い方は、図形デザインの領域でしょうし、その他(D)もあるでしょう。
今回は、(B)の使い方にあたる歴史上の世界人口の推定と予測データを使った「分布をみる散布図」を作成してみます。使用する歴史上の世界の推定人口データは、複数の研究者の公表値が記載されているWikipediaのWebサイトのデータです。
ある西暦における総人口の真値は存在していますので、グラフ上にプロットしても、相関の有無を調べる散布図でないのは確かです。
すなわち、この歴史上の人口推移の散布図は、「相関の有無をみる散布図」ではなく、ある西暦における人口の位置関係をみる「分布をみるための散布図」といえます。
散布図は、この様に、相関性をみる2つの変数データを対象にするのではなく、推定人口のような複数の研究者視点でのデータが存在する場合に、世界の総人口が歴史とともにどう変化してきたのかを目視するには、有効な手法といえます。
「相関をみる散布図」ではなく、「分布をみる散布図」の使い方といえます。
「相関をみる散布図」と「分布をみる散布図」
まずは、散布図の一般的な使い方をみてみましょう。
2つの変数の相関を調べる「相関をみる散布図」
「相関をみる散布図」は、2つのデータの関係性を見るのに作成されます。
そのデータの分布パターンにより、関係性があるのか無いのか(相関があるのか無いのか)を視覚的に捉えることができます。
その2つのデータのパターンには、
・「正の相関がある」
・「負の相関がある」
・「相関がない」
に分かれます。
相関がある場合でも、その関係性が強いのか、弱いのかといった情報も相関図から読み取ることができます。ただし、相関関係があるとみられる場合でも、その2つのデータが互いの因果関係があることを示しているわけでありませんので注意が必要です。
Excelで散布図を作成する場合には、データの分布に対して近似曲線を挿入するオプションがあります。オプションの近似曲線は、指数近似、線形近似、対数近似、多項式近似、累乗近似、及び移動平均です。移動平均以外は、近似曲線の数式、R-2乗値(決定係数)が表示できます。
散布図を作成する場合には、『作成の目的』を明確にする必要があります。
それによって、散布図の“見せ方”、“見え方”が変わってきます。
作成目的に明確にすることが重要なポイントになります。
【相関をみる散布図】県別人口増減率と老年人口比率の関係
日本は、人口減少のフェーズにはいっています。
若者が多い社会と、老年者が多い社会では、今からの人口減少はどう違いでしょうか?
次の2つの変数データで、その関係性を見てみましょう。
・データ1)現在(2025年)の都道府県別の老年人口比率(※1)
・データ2)現在から20年後、都道府県別の人口増減率
※1)老年人口比率:老年人口(65歳以上人口)の総人口に占める構成比
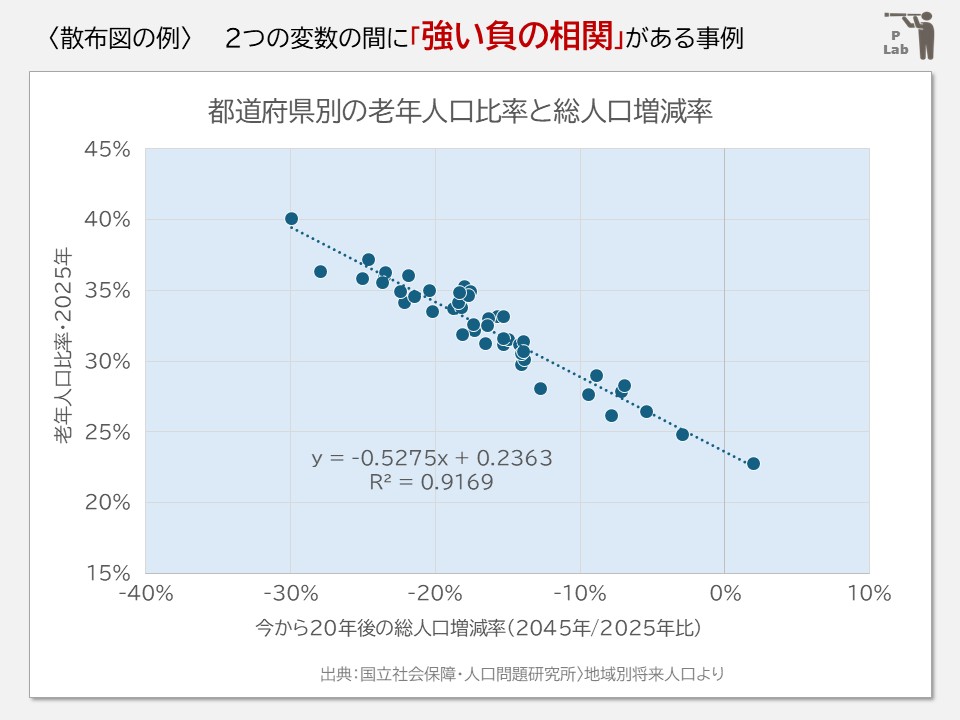
散布図から、
・現在の老年人口比率が高い都道府県ほど、20年後の総人口減少率が大きい。
・線形近似の決定係数(R2)は1に近いので回帰線の精度がたかく、「強い相関」がみられます。
この相関は現在の日本社会に当てはまっていますが、その他の社会(規模、地域、時代等々)によりその相関の有無や強弱は異なってきます。
ちなみに、最も左上の点は秋田県、最も右下の点は東京都です。
【相関をみる散布図】県別所得と進学率の関係
「相関をみる散布図」の事例として、次に、県別の高校卒業生の進学率と、その県の1人あたりの県民所得の関係をみてみましょう。
2つの変数データは、
・1人あたりの県民所得(2021年度・単位千円)
・高校生の進学率(2023年・単位%)
(データの年度の違いはご容赦願います)
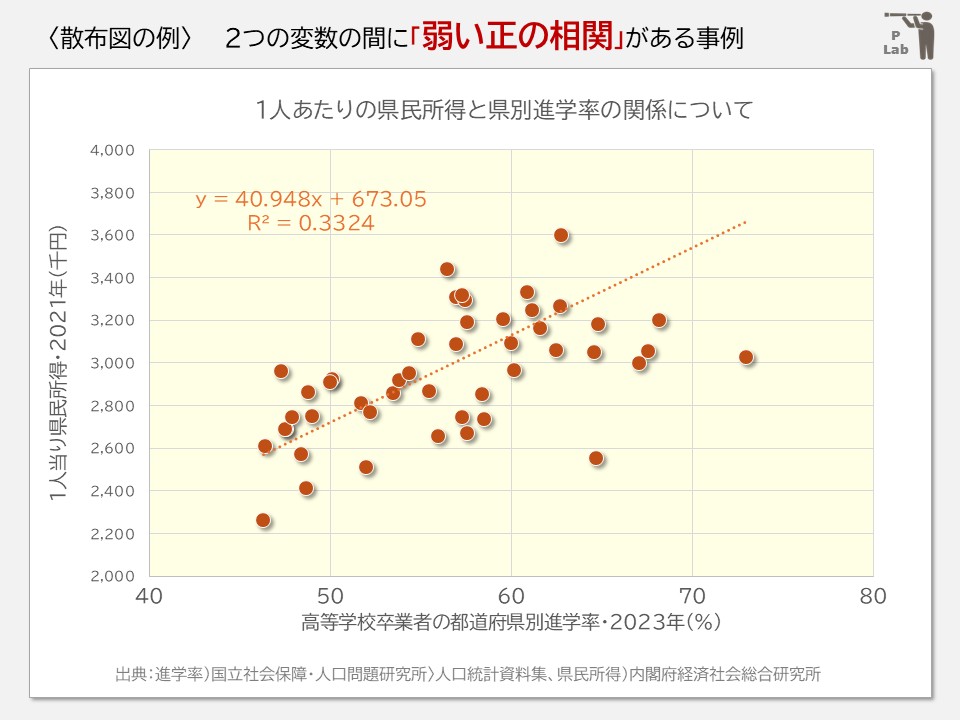
2つの変数のデータをプロットしています。
散布図に線形近似のラインをいれていますので、県民所得が高い方が進学率が高いようにもみえます。
ただし、県民所得300万円の位置する点を横軸方向にみると、進学率は47%から73%まで大きくばらついて分布しています。近似曲線(線形近似)のラインがなかったら、関係性があるようにみえるでしょうか?
散布図は、何を意図して、表現するかで散布図の見え方も変わってきます。
実は、このグラフは、東京都(1人あたり所得576万円、進学率73%)のプロットを範囲外にしています。すなわち、縦軸の範囲を200万円~400万円に変更して作図しています。一度この東京都のデータが表現される縦軸目盛(例えば、200万円から600万円)の散布図を作成してみてください。
散布図の”作成の意図”という意味が分かるでしょう。
人口推移グラフは「折れ線グラフ」か「相関図」か?
人口推移グラフは、「折れ線グラフ」、「面グラフ」、「棒グラフ」が一般的です。
詳細は、下記のサイトご覧ください。
今回の次のデータで示される、歴史上の世界の総人口の推定値と予測値に関するグラフです。
このデータを表すには、「散布図」が適切でしょう。
複数の2変数の「分布をみる散布図」
歴史上の世界総人口については、Wikipediaを出典先としています。

このサイト内に、世界人口推定・予測値として、表が記載されています。
表の内容について、研究者毎の推定年度、推定及び予測西暦範囲、データ数を下記に示します。
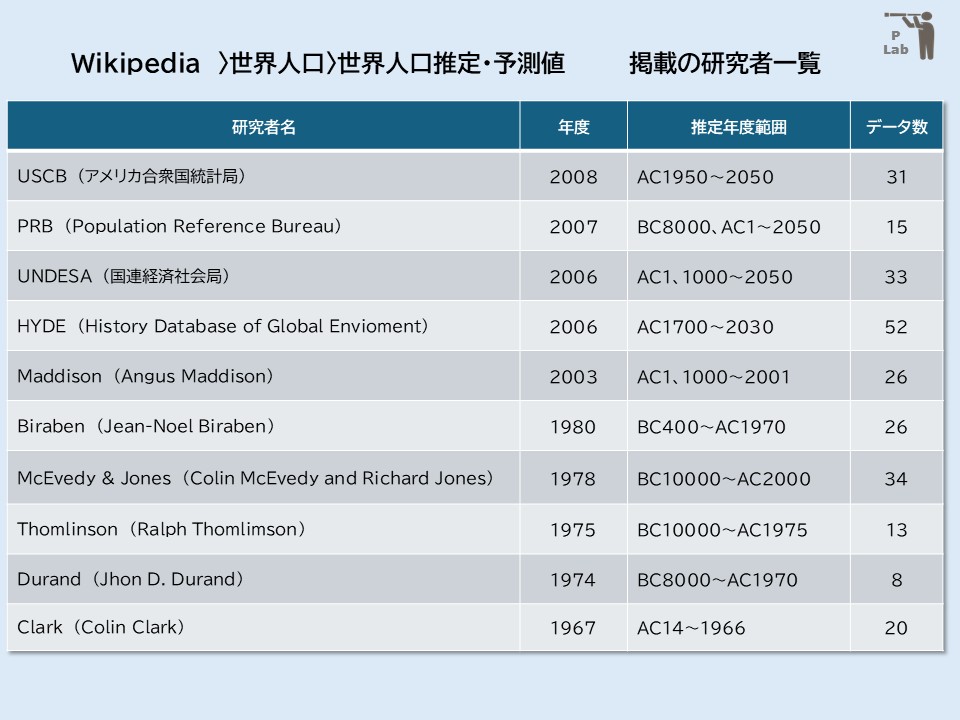
それでは、このWikipediaのデータをもとに、歴史上の世界総人口の推定及び予測値を表す散布図(「分布をみる散布図」)を作成してみましょう。
Excel「分布をみる散布図」の使い方
散布図に使う人口データ
Webサイトでは、下記のデータが示されています。
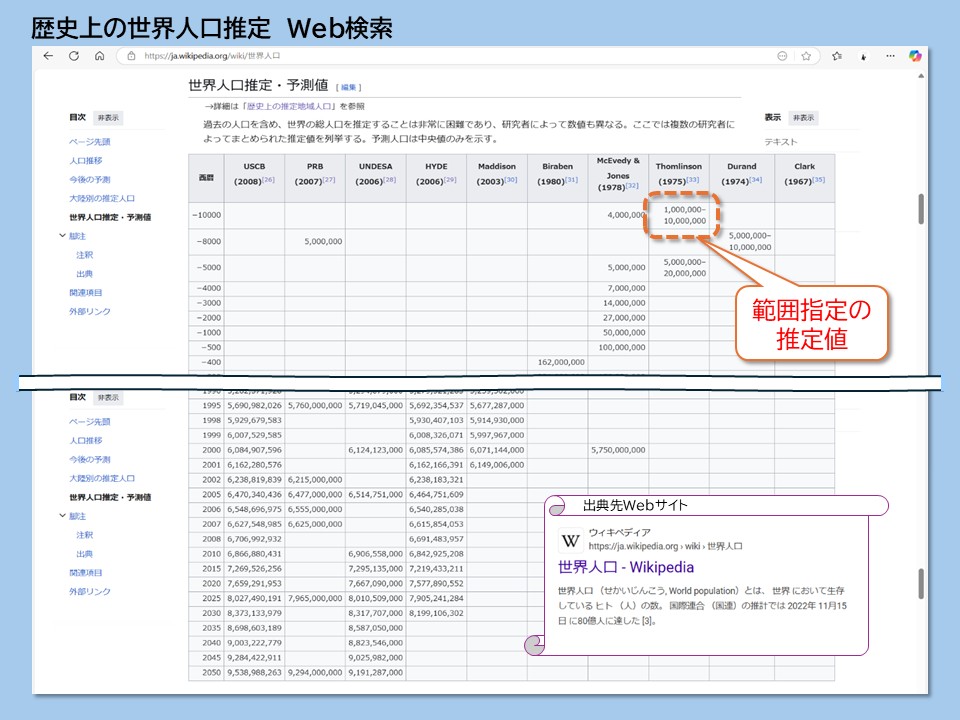
Excelで散布図を作成するために、新たにExcelのシートにコピーしましょう。
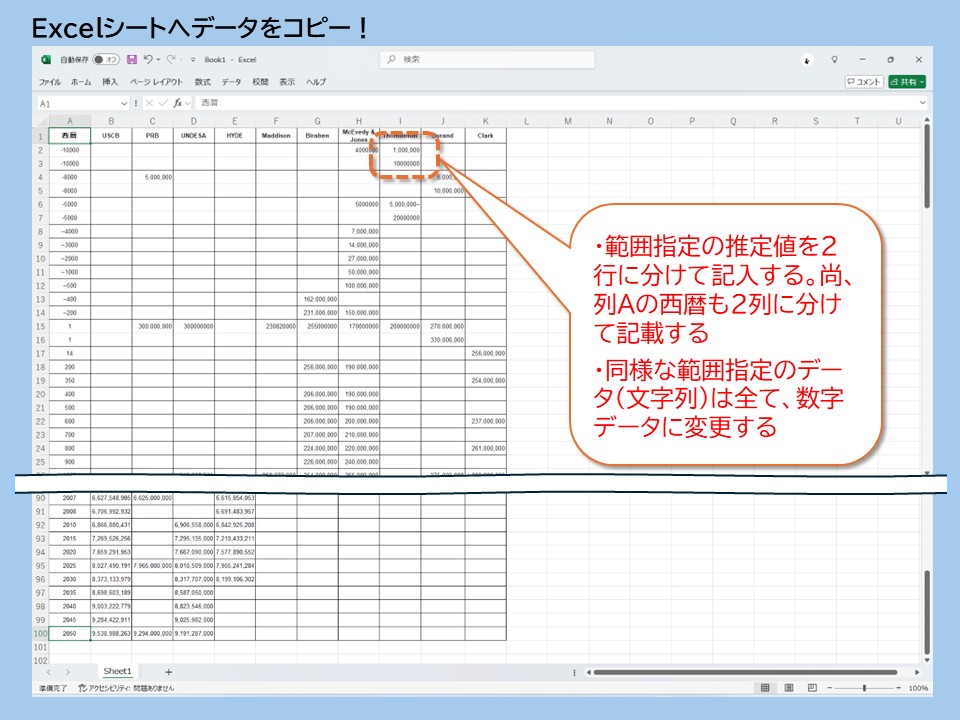
〈Excelシート上にコピーするときのワンポイント〉
・説明図1)のWebサイト上、左上の「西暦」の欄から、研究者「Clark」の最下段に右下2050年の欄までをすべてドラッグして、コピーします。
・説明図2)データは、Excelシート上のセルA1からセルK100までにコピーされます。
→コピーしたデータには、文字列となっているセルがあります。例えば、研究者Thomlinsonの西暦-10000年の推定値は、1,000,000~10,000,000人を範囲で予測しています。そのままのデータでは、文字列扱いになるため修正が必要です。
→説明図2で示すシートでは、セルI2及びセルI3に推定人口を、セルA2、セルA3には西暦-10000を記入しています。
それでは、次にExcelシート上のデータを使用して「分布をみる散布図」をみていきましょう。
散布図作成ワンポイント
Excelシート上のデータ(セルA1~K100)の範囲を指定して、挿入操作で散布図をしてぐらふを作成します。作成された散布図を説明図3に示します。
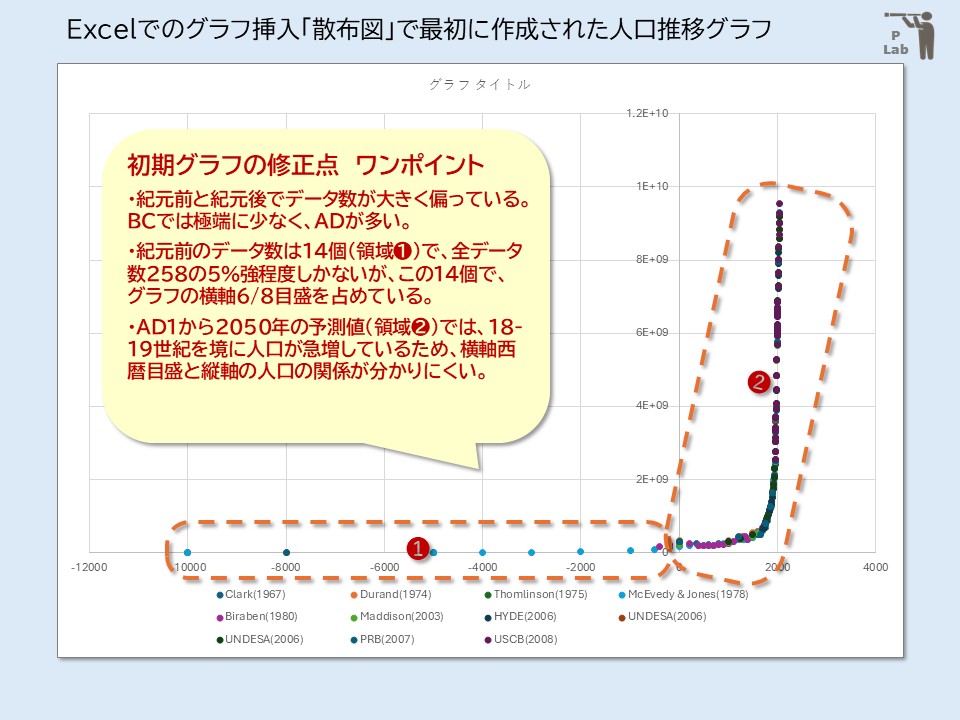
〈分布をみる散布図、作成時のワンポイント〉
・Excelのグラフ挿入では、入力されたデータをもとに、縦軸と横軸が適切な範囲で”自動的に”作成されます。自動的に作成されたグラフで、まず全体像を把握します。
・作成の目的が、「歴史上の世界人口の推移を知る」としても、説明図3のグラフでは次の点のデータを散布図から読み取ることが出来ないでしょう。
→西暦-10000年から紀元前の期間の、例えばBC-5000年の人口は何人か?を読み取ることができません。プロットはありますが、読み取ることができません。
(加えて縦軸目盛は10^9人即ち10億人単位です)
→西暦1から2000年の間、特に後半に人口が急増していますが、例えば20億人を超えたのは西暦何年?を読み取ることができません。
それでは、次に、見やすい「分布をみる散布図」について考えます。
見やすい「分布をみる散布図」の2つの方法
ここでは、見やすいグラフにする方法を2つの目的にそって紹介します。
A)「歴史全体が分かる散布図」を目的とした場合
B)「西暦と人口が読み取れる散布図」を目的とした場合
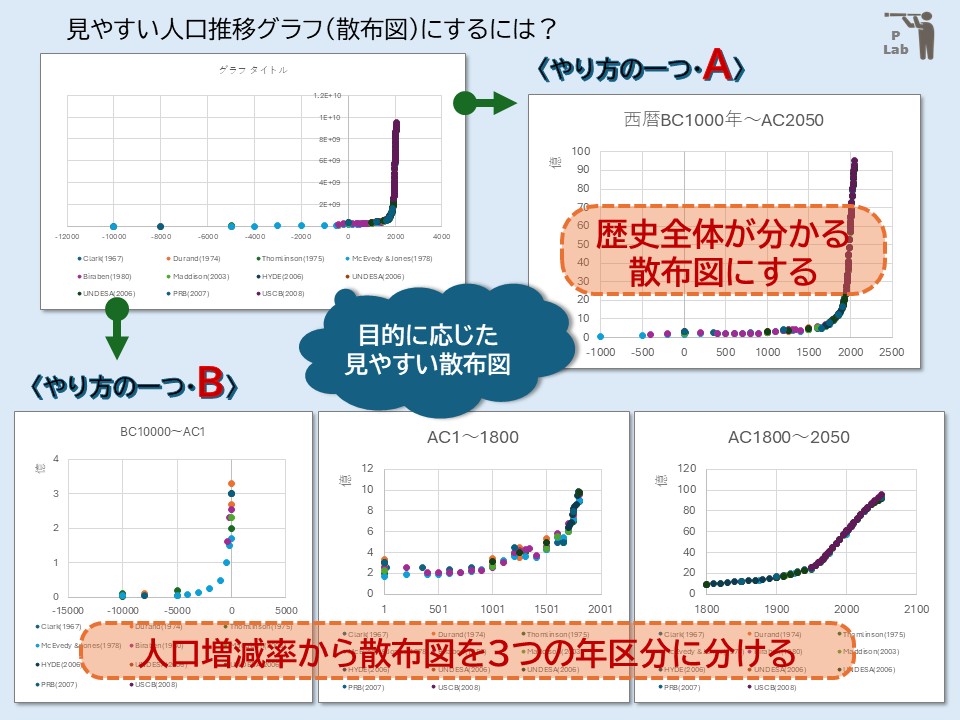
Aの目的の場合には、横軸の西暦のうち、紀元前の推定値データは一部あきらめざるを得ないでしょう。
Bの目的の場合には、データを2区分又は3区分に分割して作成する方法の紹介です。
データを観察すると、西暦-10000年から2050年の間で、人口が急増する時期が紀元前1000年前後と西暦1700~1800年頃とみて取れます。
このため、Bの場合には3つのグラフで分けて作成することにしています。
見やすい歴史上の世界人口推移グラフ
1枚の散布図で表す「歴史上の世界人口推移グラフ」
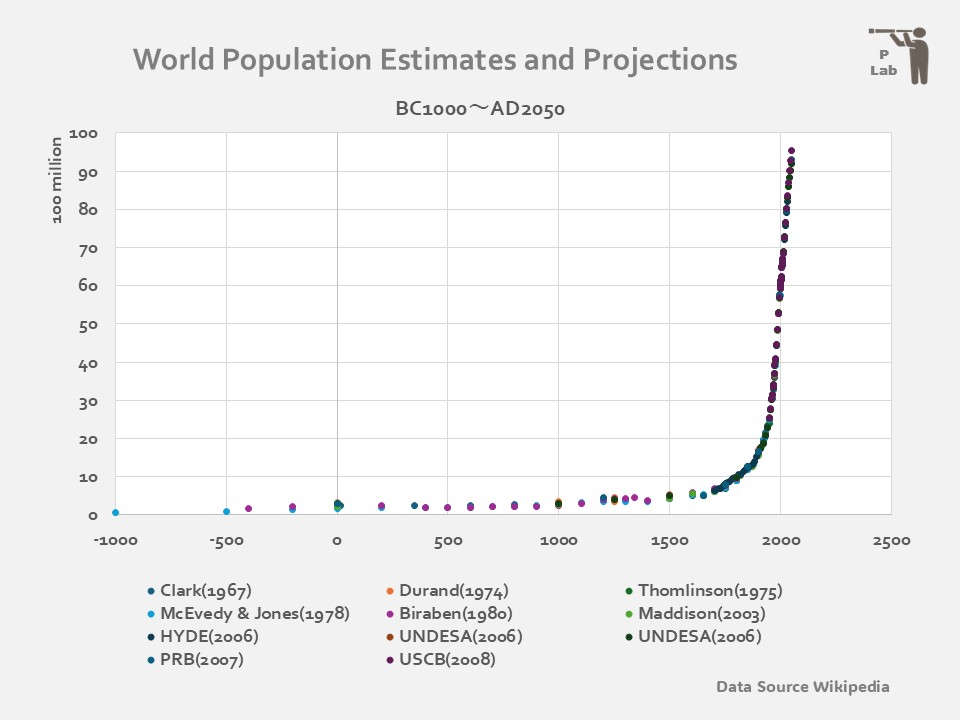
前章のAに沿った散布図です。
西暦の範囲は、BC1000年以降としています。
データはAD2050年までですが、横目盛単位を500年ピッチとしています。
3枚の散布図で表す「歴史上の世界人口推定グラフ」
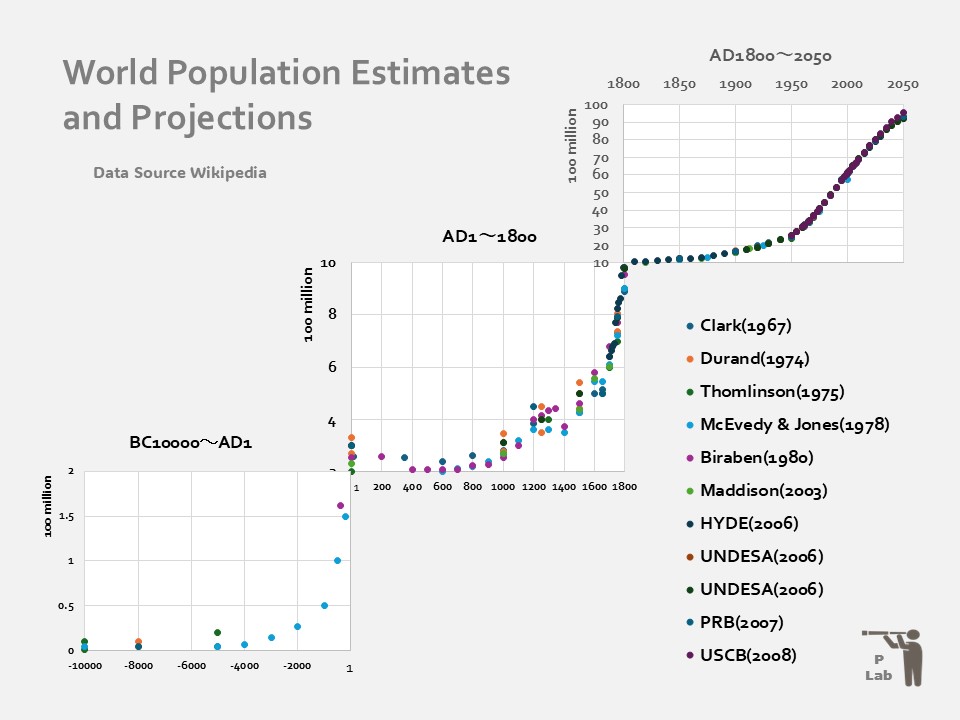
前章のBに沿った散布図です。
西暦の範囲は、Wikipediaで記載のすべてのデータをプロットしています。
3枚のグラフの起点・終点を合わせることで、見かけ上は連続した散布図となっています。
対数目盛で表す「歴史上の世界人口推移グラフ」
最後に、もう一つ散布図を示します。
縦軸を対数目盛に変更しています。
急激な人口増加がないBC500年からAD1700~1800年の間の研究者毎の推定値が見やすいグラフになっています。プロットするマーカーの色を見やすく、大きく表示しています。
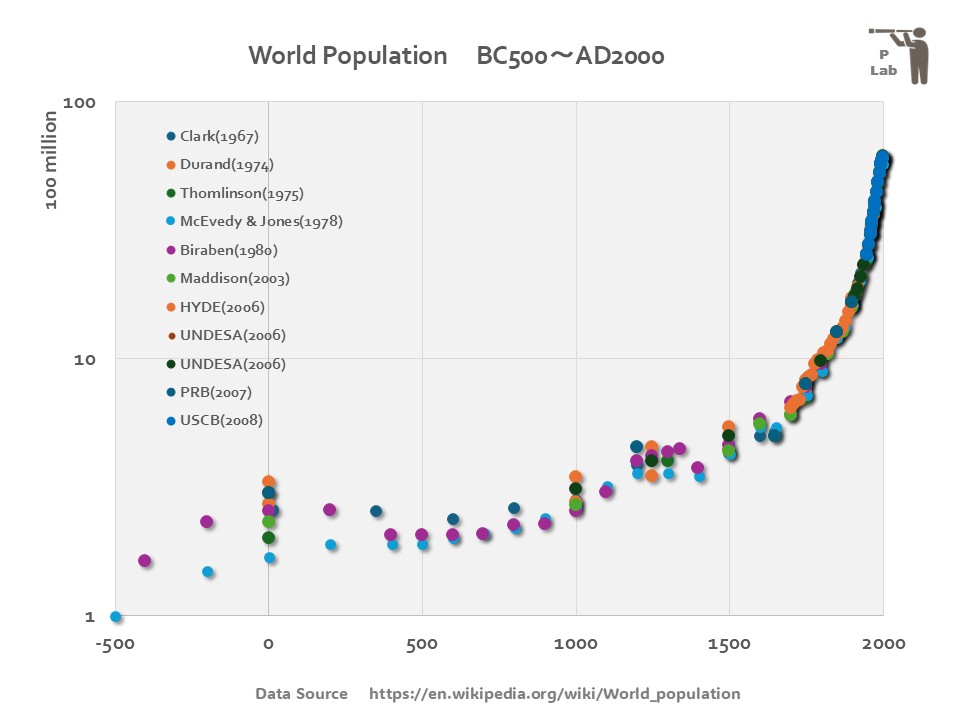
散布図で使用する機会の多い対数目盛の使用には、メリットとデメリットガあります。
デメリットは、対数目盛とした中間数値の読み取りができにくいといえます。
今回の人口推定値のデータでは、研究者による推定人口の差異がよくわかる散布図になっています。
〈出典〉 Wikipedia Webサイト>世界人口>世界人口推定・予測値
〈利用と加工〉人口動向ラボが2025年3月10日に利用し、グラフ加工しています。




